Fonctions linéaires et affines

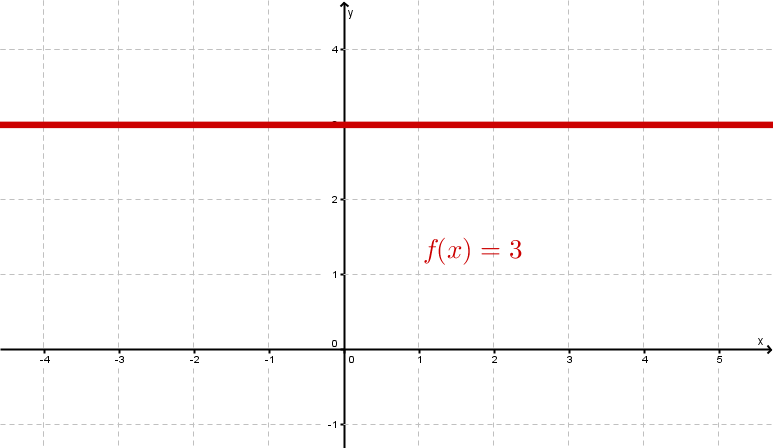
Une fonction affine est une fonction avec la forme $f (x) = m \cdot x + b$ . Sa représentation graphique est une ligne droite.

Équation générale: $f (x) = m \cdot x + b$

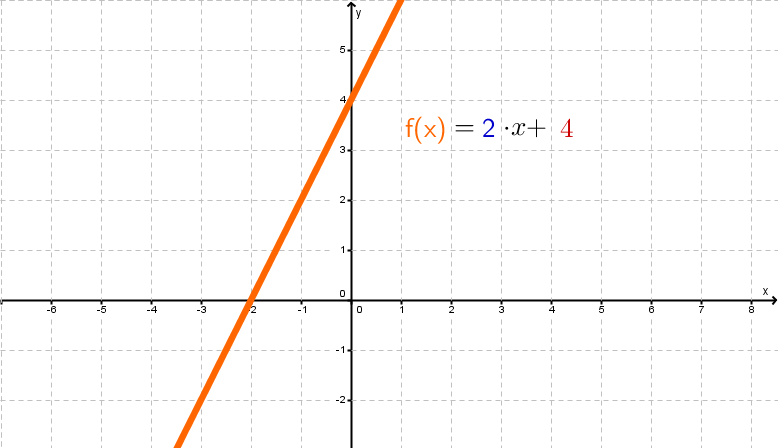
Explication des nombres dans l'équation générale

Le nombre $m$ avant la variable $x$ indique la pente und le gradient de la fonction.

Le gradient peut être lu sur le graphique à l'aide du triangle de gradient :

m = \frac{Δ y}{Δ x}

Dans l'exemple, le gradient est:

m = \frac{Δ y}{Δ x} = \frac{4}{2} = 2.

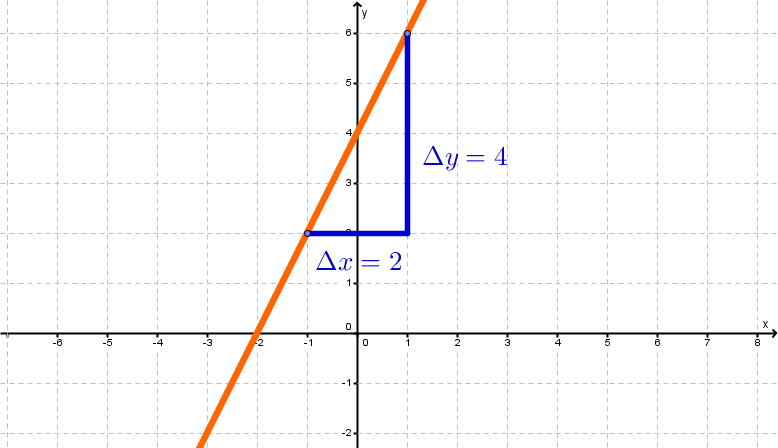
Le nombre $b$ indique l'interception de la fonction sur l'axe $y$ , donc la valeur de la fonction à $x = 0$ .. Il est appelé l'ordonnée à l'origine.

Le graphique de la fonction coupe donc l'axe des y au point $(0, b)$ .

Si la fonction affine $f (x) = m \cdot x + b$ a le nombre $b = 0$ elle est appelée fonction linéaire

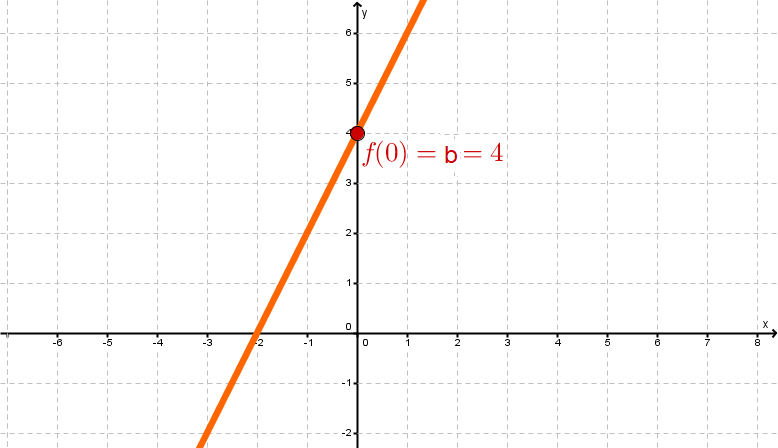
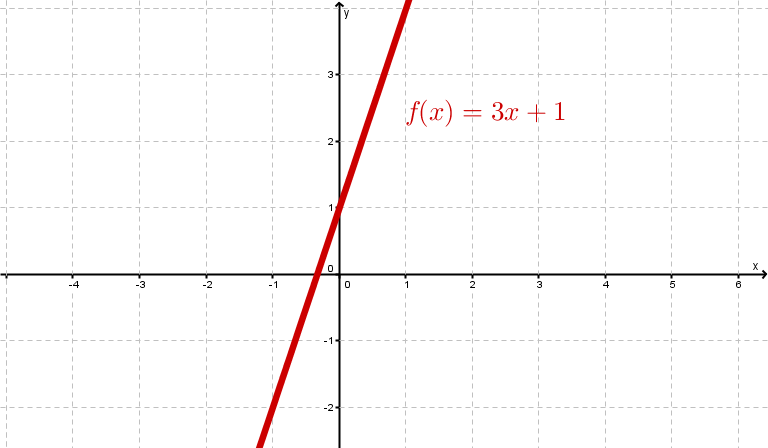
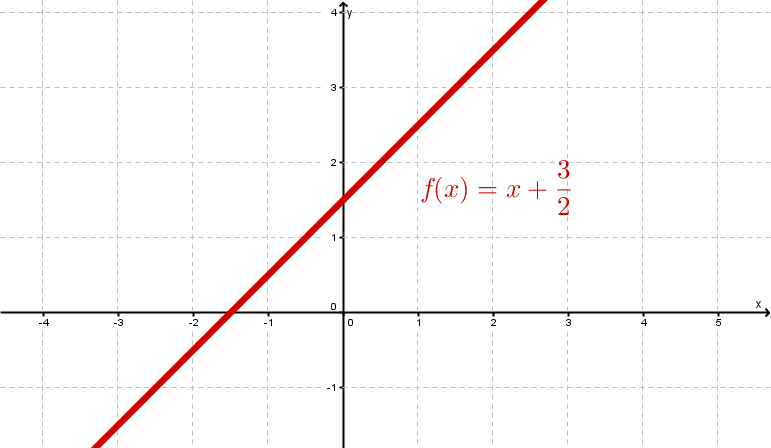
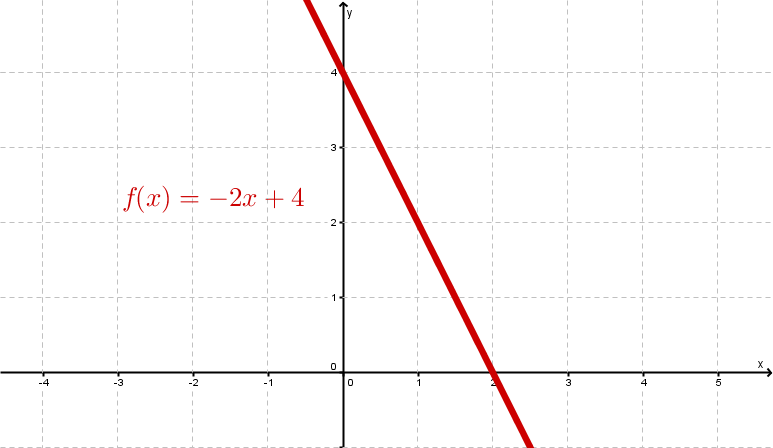
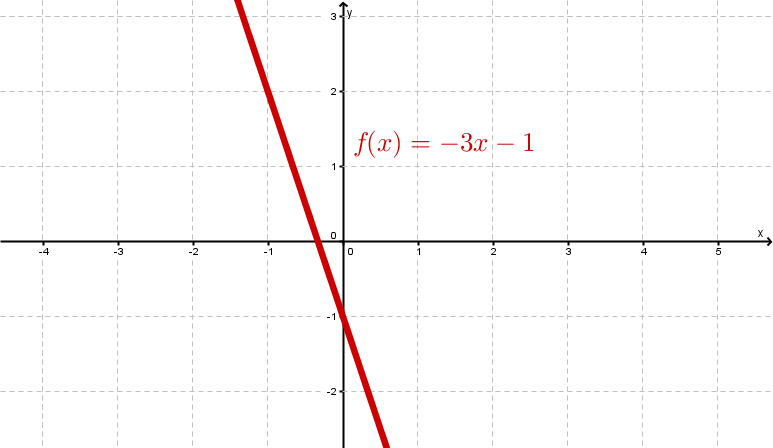
Examples

$f (x) = 3 x + 1$

$f (x) = x + 1,5$

$f (x) = - 2 x + 4$

$f (x) = - 3 x - 1$

$f (x) = 3$

Ce contenu est sous licence
CC BY-SA 4.0 → Information